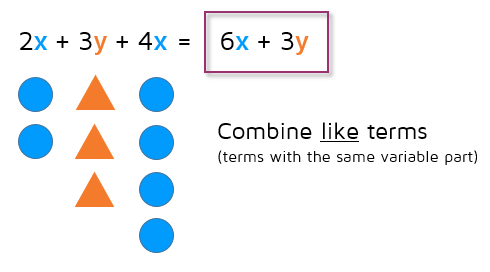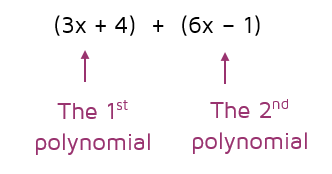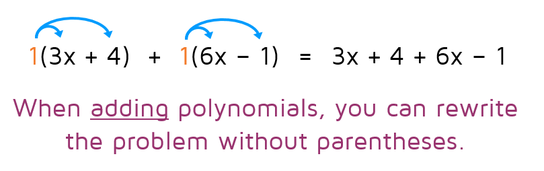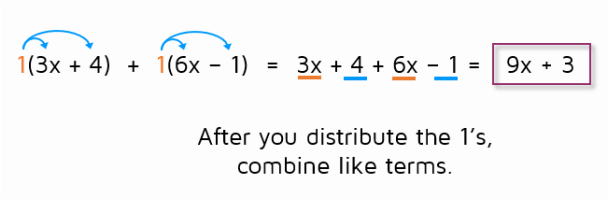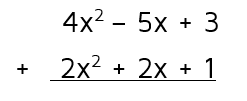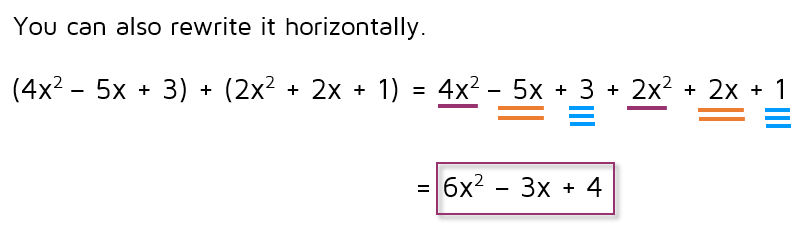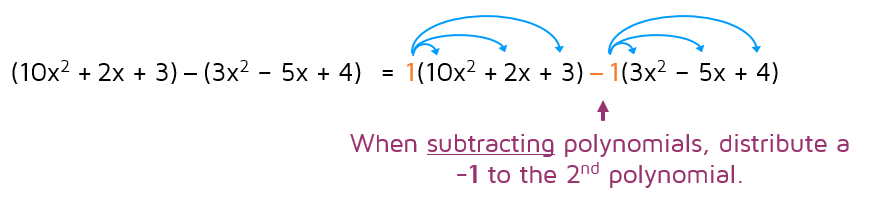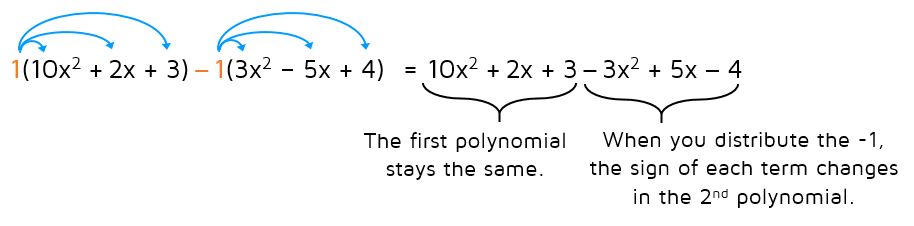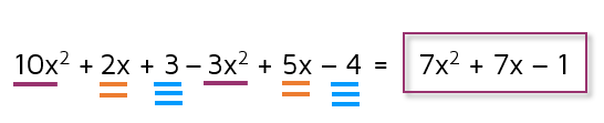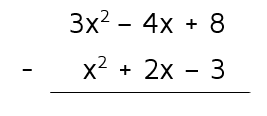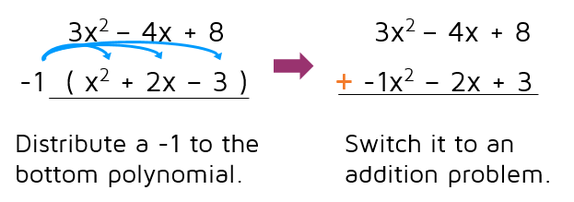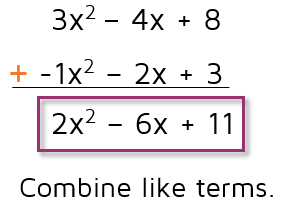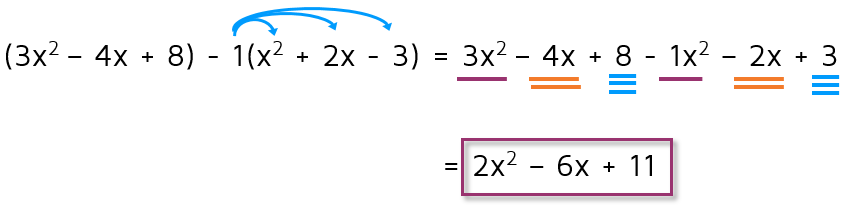​What are Like Terms?

In order to add or subtract polynomials, it's important to understand like terms first.  Like terms are terms that have the exact same variable part, they must have the same variables raised to the same powers.  Like terms can have a different coefficient (the number in front of the variable), but the variable parts must match exactly.

You can only combine terms together if they are like terms.  If they aren't like terms, you have to keep them separate.  To add like terms together, you add the coefficients and keep the variable part the same.  For example, if you're adding 4x + 3x you need to count up the x's.  There are 4 x's to start with and then you're adding 3 more x's.  This means you have 7x.  You add the 4 and the 3 together, the variable part stays the same.

​
A common mistake is for students to change the variable part when adding.  A common error when adding 4x + 3x would be to put an x-squared in the answer.  The exponent never changes when you're adding or subtracting (if you're multiplying or dividing, that's a different story).

If it helps, you can think of each variable part as a specific shape.  Let's say you have 2x + 3y + 4x.  You could think of the x's as circles and the y's as triangles.  So you would have 2 circles + 3 triangles + 4 more circles.  You can only combine terms if they have the same variable part, or in this case, the same shape.  This would mean you have a total of 6 circles and 3 triangles: 6x + 3y.  If terms are not like terms, you can't combine them together and you just leave them separate in your answer.

Welcome to Kate's Math Lessons!  

Teachers,make sure to check out the study guides and activities.

Here's one more example with shapes to help you visualize it.  Remember, you only add or subtract the coefficients of like terms. The variable part always stays the same when you're adding or subtracting.

​Adding Polynomials

To add polynomials, you just need to combine all the like terms. Often, the polynomials will be placed inside of parentheses to show the two separate polynomials that are being added.  For example, if 3x + 4 and 6x - 1 are being added, it might look like this:

To make this look a little simpler, we can rewrite it without parentheses.  Notice that there isn't a number written outside of the parentheses.  If we wanted to, we could put a 1 on the outside of each one.  If we distribute the 1, nothing happens!  When you're adding two polynomials, you can remove the parentheses and nothing will change.

After you distribute the 1, it's simply a matter of combining like terms.  The x's can be combined and the constants can be combined.

Adding Polynomials Vertically

In all of the examples above, the polynomials were written horizontally. You might be given problems where the polynomials are written vertically instead, with one written right below the other instead of side-to-side.

When you're adding regular numbers like 3 + 2, you can write the addition vertically or horizontally.  You get the same answer either way.  When polynomials are added vertically, you can just add straight down if the terms are lined up in order. 

You can rewrite the problem horizontally if you prefer.  You get the same answer either way.

​
Subtracting Polynomials

Be extra careful when subtracting polynomials.  If you want to get rid of the parentheses, you need to distribute a negative 1 to the second polynomial.  

The first polynomial will stay the same because nothing happens when you multiply by a positive 1.  When you distribute the negative 1 to the second polynomial, it will change the sign of each term.
​

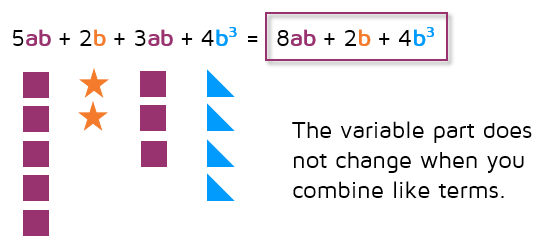
After you distribute to rewrite the problem without parentheses, all that's left to do is to combine like terms.  Remember, you add or subtract the coefficients of like terms only.  The variable part does not change when you combine like terms.  If terms do not have the same variable part, you cannot combine them together.

By the way, it's completely up to you how you want to mark like terms on your paper.  Some students like to draw different shapes around each set of like terms.  You can color code them if you have colored pencils.  Some students like to cross them out as they go, it's completely up to you.

Subtracting Polynomials Vertically

Be extra careful when subtracting polynomials vertically.  You can subtract straight down if the like terms are lined up.  However, students tend to make more mistakes when subtracting as opposed to adding, especially if negative numbers are involved.  Our advice is to distribute a negative 1 to the bottom polynomial and then add the terms instead.  

Let's say you've been given this subtraction problem:

You could subtract straight down since the like terms are lined up. If you choose to do this, be very careful to subtract at each step.  A common error is to subtract for the first set of like terms and then to accidentally switch to adding for the rest of the problem.  An easy way to avoid this is to distribute a negative 1 to the bottom polynomial first to switch it to an addition problem.  You don't have to do this step, but most students find it easier to add instead of subtract.

Now that it's been rewritten as an addition problem, we can add all the like terms together in each column.

You can also rewrite the problem horizontally if you want to.  You can see below that you get the same answer.  

It does not matter whether you choose to write the problem vertically or horizontally.  Pick the method that seems easiest to you.  Make sure to be extra careful when subtracting polynomials - pay close attention to positive and negative signs.

Practice

Ready to try a few problems on your own? Click the START button below to try a practice quiz.

Powered by Interact